🧠 디지털 가든

Q01. 통계학은 어떤 학문인가?

8 min read

요약

  • 통계학은 크게 기술 통계와 추론 통계로 구분된다.
  • 기술 통계란 다양한 통계량(평균, 분산, 첨도, 왜도 등)을 통해 데이터의 특징을 기술한다.
  • 추론 통계란 샘플 데이터의 특징을 확인하고, 통계 모델링을 통해 모집단의 특징을 가정하고 이를 추론한다.

1. 통계학이란?

통계학이란 가장 큰 카테고리는 기술 통계와 추론 통계로 구분된다. 통계학에서 거의 모든 영역에서 다루는 문제는 이 두가지 관점 내에서 이해할 수 있다.

2. 기술 통계

기술 통계

  • 기술 통계(desriptive statistics)란 데이터 특징을 기술(묘사)하는 것으로 크게 3가지로 구분된다.
  • 중심 경향치는 데이터가 특정 값에 집중되는 정도를 나타내는 지표를 의미한다. 대표적으로 평균, 중앙값, 최빈값 등이 있다.
  • 흩어짐 정도는 데이터가 얼만큼 모여 있는지 흩어져 있는지 나타내느 지표를 의미한다. 대표적으로 분산, 표준편차, 평균절대편차 등이 있다.
  • 분포는 데이터가 어디에 몰려 있는지 퍼져 있는지 나타내는 지표를 의미한다. 대표적으로 치우침 정도인 왜도와 뾰족함 정도인 첨도가 있다.

2.1 중심 경향치

데이터가 어떤 값에 집중되는 정도

  1. 평균
    1. 가장 흔하게 사용되는 중심 경향치 값
    2. 각 샘플 별로 중요도가 동일하다고 가정
    3. 샘플 합 / 개수
  2. 중앙값
    1. 이상치의 영향으로 평균이 샘플을 대표하지 못하는 경우 사용
    2. 샘플의 중간에 위치한 값(짝수 개인 경우 중앙 2개의 값에 대한 평균)
  3. 최빈값
    1. 수치로 나타내지 못하는 카테고리 값의 경우 사용
    2. 가장 빈도가 높은 값

2.2 흩어짐 정도

데이터가 얼마나 흩어지고 퍼져 있는 정도. 데이터의 집중 정도가 동일해도 흩어짐 정도가 다를 수 있다.

  1. 분산(variance)
    1. 분산이 작으면 샘플들이 평균 근처에 몰림
    2. 편차제곱합에 대한 평균
      1. 편차(deviation)란, 개별 샘플 값 - 샘플 평균()
      2. 제곱합 Why? 일반 편차를 더하면 0이 되어버려서 척도로 활용 불가능
  2. 표준편차(Standard Deviation, SD)
    1. 분산의 제곱근
    2. 앞서 계산한 편차에 제곱한 값을 다시 되돌리는 느낌으로 표준 편차
  3. 평균절대편차(Mean Absolute Deviation, MAD)
    1. 편차 절댓값 합에 대한 평균

2.3 분포

데이터가 어떻게 퍼져 있는지 측정하여, 특정 값이 얼마나 자주 또는 드물게 등장하는지 패턴을 보여준다.

  1. 왜도(skewness) ^435d11
    1. 데이터 분포의 좌우 비대칭성을 나타내는 척도
    2. 왜도 = 0: 좌우 대칭
    3. 왜도 > 0: 우측 왜곡(right-skewed)
      1. 그러나 실제 데이터는 왼쪽에 몰려있음
      2. Why? 가장 흔하게 사용하는 피어슨의 최빈값 왜도 계수로 이해
      3. 데이터가 왼쪽에 몰려있으면 평균 > 최빈값 으로 왜도 계수가 0보다 크다
  1. 첨도(kurtosis)
    1. 데이터 분포의 뾰족함이나 완만함을 나타내는 척도
    2. 첨도가 클수록 데이터 분포가 뾰족함
    3. 기존 첨도의 경우 3인 경우 정규 분포를 나타냄
    4. 그러나 기존 첨도에 3을 빼서 0인 경우 정규 분포를 나타내게 하는 초과 첨도(excess kurtosis)를 직관적으로 사용

3. 추론 통계

추론 통계

  • 추론 통계는 모집단 일부인 샘플 데이터를 추출한 후 샘플 데이터를 바탕으로 통계 분석을 통해 모집단을 추론한다.(기술 통계와 구분되는 새로운 관점)
  • 추정은 데이터와 가장 잘 맞는 통계 모델을 학습하는 빈도주의(예. 최대우도추정)와 사전 지식에도 잘 부합하는 통계 모델을 학습하는 베이지안(예. 최대사후확률추정)이 있다.
  • 가설 검정은 샘플 데이터를 통해 설정한 가설이 통계적으로 유의미한지 검정하는 것으로 귀무가설에 따라 양측 검정과 단측 검정으로 구분한다.

샘플 데이터에도 기술 통계를 적용할 수 있으면 해당 값을 통계량이라고 한다. 이렇게 계산된 통계량으로 모집단의 통계량인 모수를 추정하는 과정이 추론 통계의 일부이다. (참고로 모수 = 파라미터 이다. 모수는 통계학에서 모집단을 강조할 때 사용되며, 파라미터는 일반적으로 수학 모델링 및 머신러닝에서 사용된다.)

3.1 추정

  1. 빈도주의
    1. 내가 보유한 데이터에 가장 잘 맞는 통계 모델을 학습하는 방향
    2. 최대우도추정
  2. 베이지안
    1. 내가 보유한 데이터에서 해당 데이터에 대한 사전 지식에도 잘 맞는 통계 모델을 학습하는 방향
    2. 최대사후확률추정

3.2 가설 검정

궁금한 문제의 특징에 따라 검정 방향이 구분된다. (참고: Q38. p-value라는 숫자가 실제로 의미하는 직관은?)

  1. 양측 검정
    1. 귀무가설에서 통계량이 특정 숫자와 동일한지 아닌지 판단할 때, 양쪽 방향을 모두 고려
  2. 단측 검정
    1. 귀무가설에서 통계량이 특정 숫자보다 큰지 작은지 검정할 때, 한쪽 방향만 고려

4. 통계학 분류표

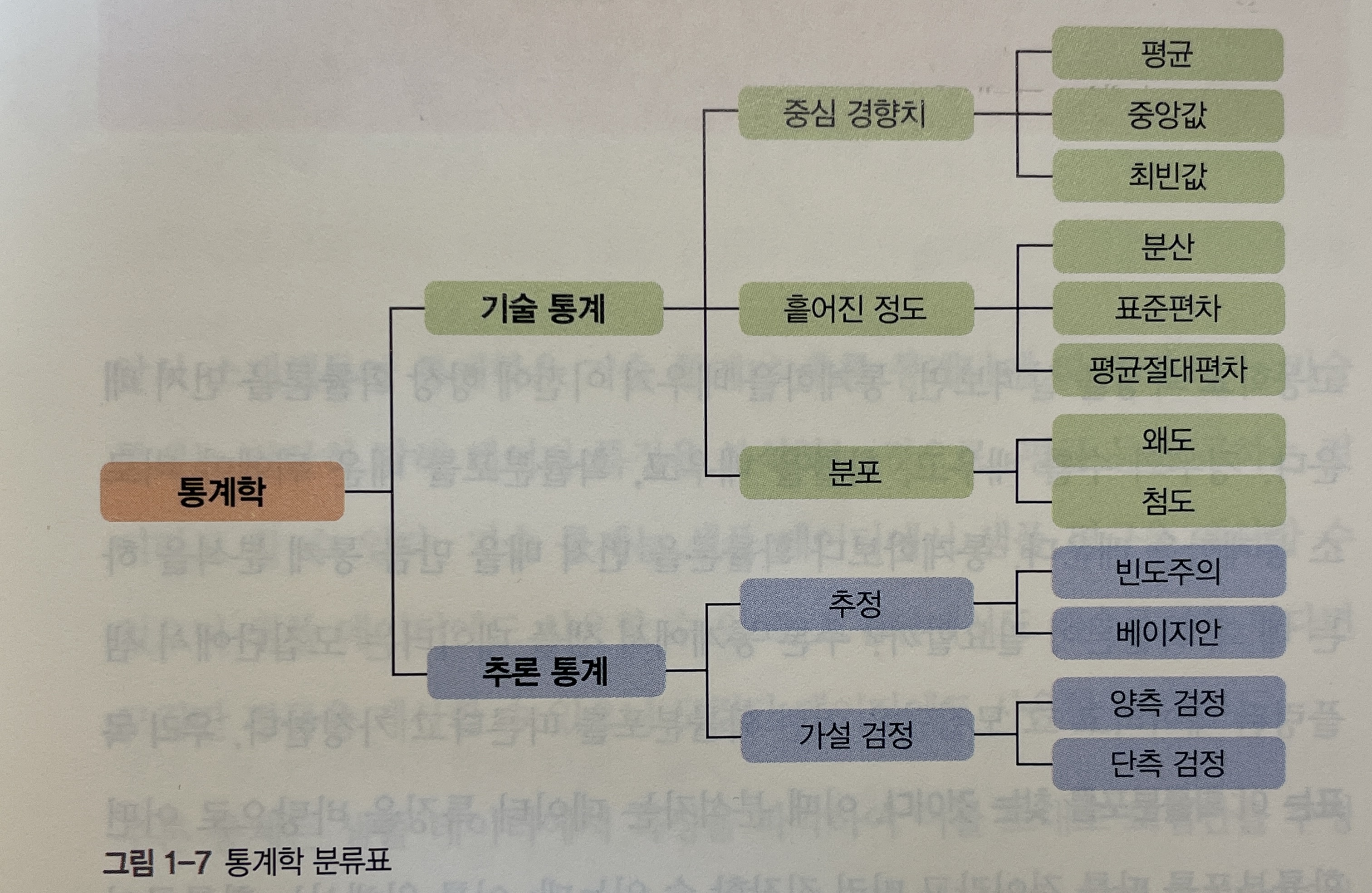
참고자료

그래프 뷰

백링크