Q08-10. 통계 분석에서의차원과 차원을 줄이는 방법은?

요약

• 샘플보다 차원 수가 많으면 문제가 커져 차원을 축소하는 통계적인 방법으로 사전 지식, 변수 간 상관관계, 부분집합 선택, 정규화, 주성분 분석 등이 있다.
• 부분집합 선택은 변수 간 조합으로 가장 성능이 잘 나오는 변수 조합을 찾는 방법이며, 대표적으로 전진 선택과 후진 제거가 있다.
• 정규화(regularization) 기법은 변수를 제거하는 것이 아닌 변수의 영향을 측정하는 계수 값을 조정하는 방법이며, 대표적으로 라쏘(L1)와 릿지(L2)가 있다.
• 주성분 분석(PCA)는 기존 변수들을 이용하여 데이터를 잘 설명하는 새로운 변수(PC)들 만 남기는 방법이다.

---

1. 현재 통계학에서 직면한 챌린지

현재 문제점

빅데이터 시대에서 샘플 수가 무수히 많으면 큰 상관이 없지만, 그 만큼 특징(feature) 수도 굉장히 많이 증가하므로 고차원 문제에서 자유로울 수 없다.

1.1 고차원 데이터

고차원 데이터(High-Dimensional Data)란?

차원(feature)과 샘플의 크기를 비교했을 때, 차원이 샘플 크기보다 크면 고차원 데이터라고 하며 이 때 차원의 저주(the curse of dimensionality)를 일으킨다.

다시 말해, 차원의 저주는 다음과 같은 경우이다. 이러한 데이터를 고차원 데이터라고 한다. 대표적으로 생물 데이터 주로 등장한다.

예를 들어 유전자 데이터의 경우, 한 사람에게 약 2만 개의 유전자 수를 보유하고 있는데 2만 명 보다 많은 사람들의 유전자 정보를 수집하기에 비용이 막대하다.

$$차원(p)>샘플수(n)$$

따라서, 차원을 줄일 수 있는 차원 축소에 대한 통계적인 방법을 이용한다.

---

2. 차원을 줄이는 방법

차원이란?

데이터 분석 관점에서 차원(Dimension)이란 간단하게 특징(feature)의 수인 입력 변수의 수로 이해하면 된다.

2.1 사전지식 활용

데이터가 실제로 어떤 의미를 지니는 지 파악하는 것으로 차원을 줄이는 데 많은 도움이 된다.

위 예시 유전자 데이터에서 주요 특정 유전자만 발현량을 확인하여 차원에 상응하는 샘플 수를 확보할 수 있다. 단, 통계 및 수학적으로 객관적인 방식이 아닌 실제 의미 자체에 집중하므로 분석자의 사전 지식 수준에 따른 리스크가 존재한다.

2.2 입력 변수 간 상관관계 파악

입력 변수들 간 관계는 독립적이어야 한다. 그래서 변수 간 상관관계를 파악하여 의존적인 특징(feature) 중 하나의 특징만 추려 차원을 줄일 수 있다.

예를 들어, 체질량지수(BMI)는 $몸무게/{키}^2$ 로 두 변수와 관계로 세 변수를 모두 활용하기에는 중복된 정보가 있다. 기존 몸무게와 키 변수를 활용하던지, 체질량지수와 출력변수 간 연관성을 파악하고 싶다면 몸무게와 키 중 한 가지를 제거하면 된다.

2.3 부분집합 선택

여러 변수가 존재할 때, 특정 부분집합만 선택하여 분석에 활용한다. 대표적으로 최적 부분집합 선택(best subset selection)이란, 모든 변수 사이에 가능한 쌍을 모두 고려하여 가장 성능이 잘 나오는 변수 조합으로 모델을 학습한다.

예를 들어 원래 차원이 $p$ 에서 입력 변수 1개만 선택하는 경우, 입력변수가 1개인 모델에서 입력 변수 $x_1,x_2,...,x_p$ 1개씩 모두 고려하여 가장 성능이 좋은 것을 선택한다.

이를 일반화 하면 차원이 $p$ 에서 입력 변수를 $k$ 개 선택하는 경우 부분집합의 경우의 수는 다음과 같다. 결국 최적 부분집합 선택은 $p$ 가 1에서 $p$ 까지 모든 경우의 수를 고려하므로 계산량이 지수적으로 증가한다.(정확히는 $2^p$ 로 증가한다.)

$${}_p{C}_k=\frac{p!}{k!(p-k)!}$$

따라서, 계산량이 너무 많아 비효율적인 최적 부분집합 선택을 보완하기 위해 전진 선택(forwoard selection)과 후진 제거(backward elimination)를 이용한다.

전진 선택

전진 선택(forward selection)이란 입력 변수를 1개씩 순서대로 추가하여 최적의 모델을 찾는 방법

아래와 같이 최적의 부분 집합 모델이 다음과 같다고 가정할 때 놓칠 수 있는 상황이 존재한다.

• $p=1$, 최적의 입력 변수: $x_1$
• $p=2$, 최적의 입력 변수: $x_2,x_3$

전진 선택 방법은 $p=1$ 인 경우 입력 변수 $x_1$가 선택되어 다음 모델에 반드시 $x_1$ 포함된다. 이로 인해 최적의 입력 변수 조합인 $x_2,x_3$을 만족할 수 없다. (단, 입력 변수가 1개인 경우의 최적의 변수는 일반적으로 입력 변수가 많은 경우에도 높은 기여를 한다.)

후진 제거

후진 제거(backward elimination)란 모든 입력 변수를 포함한 상태에서 시작하여 입력 변수를 1개씩 제거하여 성능을 크게 떨어뜨리는 변수를 제거하여 최적의 모델을 찾는 방법

후진 제거 방법에도 동일하게 적용된다. $p=2$ 인 경우 입력 변수가 $x_2,x_3$ 으로 다음 모델에는 두 변수 중 하나가 들어가서 $x_1$을 만족할 수 없다.

이러한 한계점을 보완하고자 전진 선택과 후진 제거를 동시에 고려한 단계별 선택(stepwise selection)도 존재한다.

2.4 정규화 기법

결국 앞선 방법들의 목적은 차원 축소 즉, 입력 변수들을 없애는 것이다. 위와 같은 방법으로 입력 변수들의 수를 직접적으로 조정할 수도 있지만 입력 변수가 출력 변수에 영향을 미치는 정도인 계수를 조정하여 차원을 축소시킬 수 있다.

다시 말해 아래 모델을 예로 들면, 입력 변수($x_i$)를 없애는 것이 아니라 계수(${\beta }_i$)를 줄이거나 0으로 만드는 과정을 통해서 모델 내 입력 변수($x_i$)의 영향 정도를 줄여 차원이 사라지는 간접적인 효과를 준다.

$$y={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+...+{\beta }_p{x}_p+ϵ$$

이 때, 계수(${\beta }_i$) 를 매우 감소시키는 정규화 기법을 릿지(Ridge, L2)라고 하며, 0으로 만드는 정규화 기법을 라쏘(Lasso, L1)라고 한다.

잔차제곱합(Residual Sum of Squares, RSS) 알고가기

우선, 잔차제곱합을 이야기하는 이유는 라쏘(lasso)와 릿지(ridge)에서 목적함수로 잔차제곱합(RSS)를 활용한다. 물론 다중 선형회귀에서 잔차제곱합을 최소로하는 값을 학습한다.

아래와 같은 입력 변수가 $p$ 개인 다중 선형회귀 모델이 있고, 여기에서 $i$라는 인덱스를 추갛여 구체적을 샘플 각각을 구분하였다.

또한, 은 오류라고 하는데 모집단에서는 오류가 오차가되고, 샘플 데이터에서 오류는 잔차(Residual)가 된다. 이 때 모델에서의 오류($ϵ$)는 샘플 데이터를 대상으로 이루어져 있기 때문에 잔차라고 한다.

$$y={\beta }_0+{\beta }_1{x}_{i1}+{\beta }_2{x}_{i2}+...+{\beta }_p{x}_{ip}+ϵ={\beta }_0+\sum _{j=1}^p{\beta }_j{x}_{ij}+ϵ$$

즉, 잔차(Residual)는 다음과 같아지며, 이때 잔차제곱합(Residual Sum of Squares,RSS)는 $i$번째 샘플들에 대한 잔차들을 각각 제곱하여 모두 더한 값이다.

이러한 잔차제곱합(RSS)에 대한 최솟값 문제는 다중 선형회귀 뿐만 아니라 라쏘나 릿지에서도 활용된다.

$$\begin{array}{rl}& Residua{l}_i=\left(y_i-{\beta }_0-\sum _{j=i}^p{\beta }_j{x}_{ij}\right)\\ & \\ & RSS=\sum _{i=1}^n{\left(y_i-{\beta }_0-\sum _{j=i}^p{\beta }_j{x}_{ij}\right)}^2\end{array}$$

2.4.1 라쏘와 릿지

라쏘와 릿지가 최소화시켜야 하는 목적함수는 위 잔차제곱합(RSS)이고, 제한 조건(Limit Codition, LC)은 각각 아래와 같다.

• 라쏘(Lasso, L1): 파라미터들의 절댓값 합이 특정 상수 값 이하
• 릿지(Ridge, L2): 파라미터들의 제곱값 합이 특정 상수 값 이하

$$\begin{array}{rl}Lass{o}^{\prime }sLC& =\sum _{j=1}^p|{\beta }_j|\le c\\ Ridg{e}^{\prime }sLC& =\sum _{j=1}^p{\beta }_j^2\le c\end{array}$$

이해를 위해 계수 $\beta 1,\beta 2$ 에 대한 아래 그림을 비교하자. 제한 조건이 없을 때 목적함수 잔차제곱합(RSS)의 최적해 검은색 포인트이고, 제한 조건이 있을 때 최적해의 범위는 마름모 또는 원 모양의 빨간색으로 색칠된 부분에 존재해야 한다.

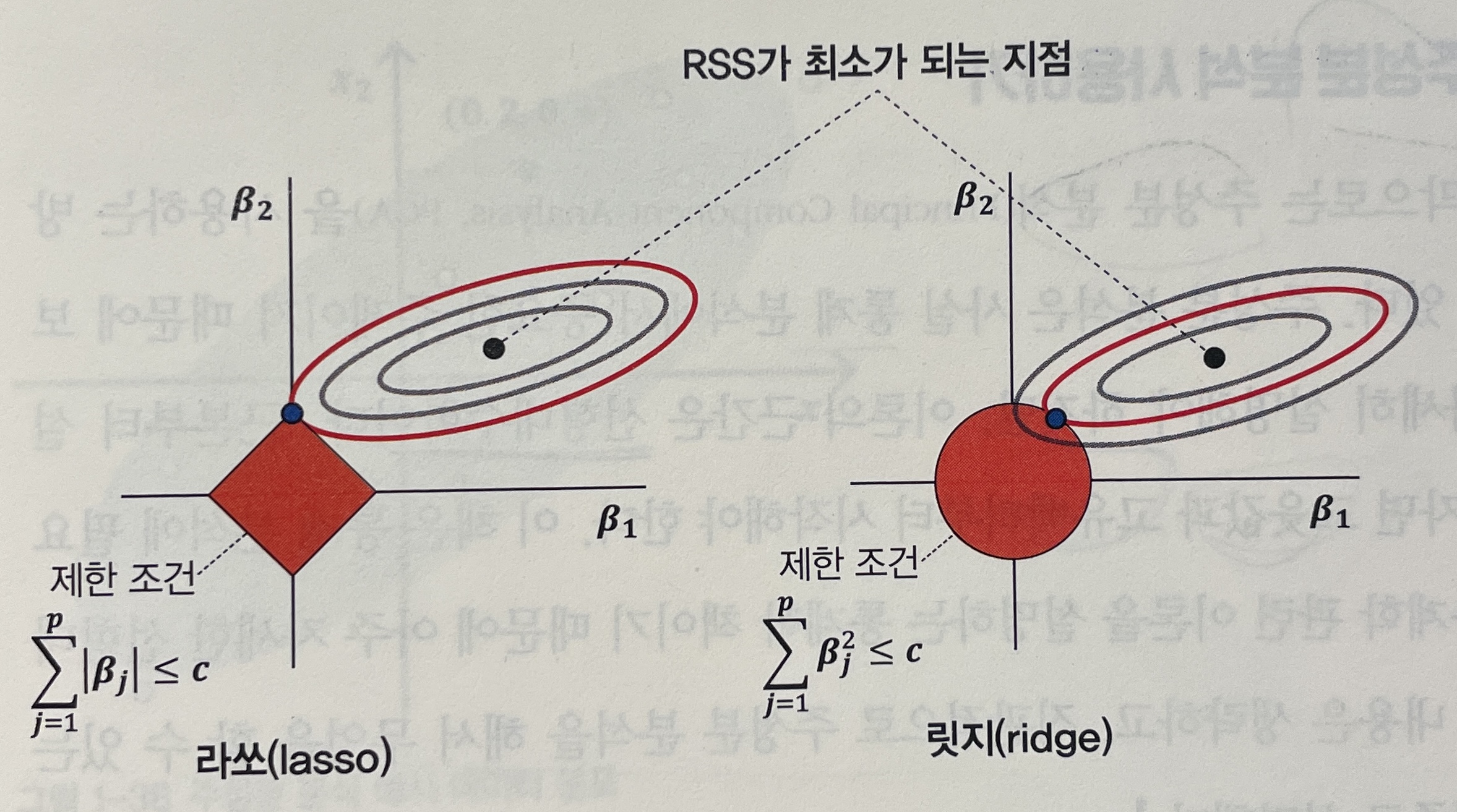
이처럼 라쏘(lasso)의 경우 최적해 조합은 ${\beta }_1=0$ , ${\beta }_2$는 특정 상수 값이다. 이처럼 극단적으로 특정 계수의 값을 0으로 만들면서 입력 변수가 출력 변수에 아무런 영향을 주지 않도록 한다.

반면에 릿지(ridge)는 ${\beta }_1$ 값이 작지만 어느 정도 값을 유지한다. 그러나 제한 조건이 없을 때의 최적해였을 때의 ${\beta }_1$값 보다는 매우 감소시켜 출력 변수에 미치는 영향을 줄인다.

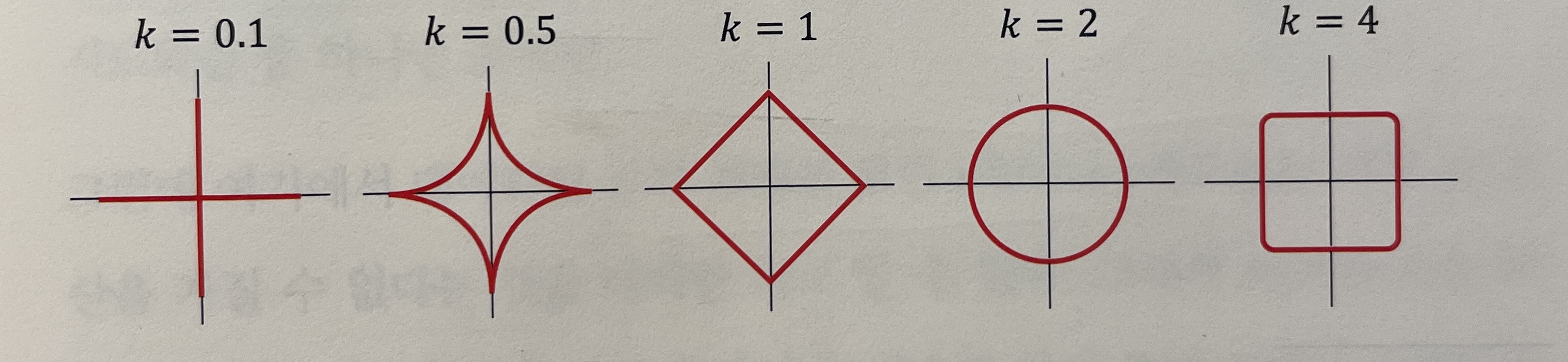
단, 라쏘에서 항상 마름모의 꼭지점이 최적해를 가지는 것이 아니라 애매한 영역에 존재할 수 있다. 다만 원보다 마름모 형태일 때 한쪽 파라미터 값을 무시할 정도로 작아지게 한다. 이처럼 극단성을 조절하는 값을 노름(norm, = $k$)이라고 한다. 즉, $k$ 값이 작아질수록 극단적으로 변수 선택하는 경향이 높으며 보통 라쏘($k=1$), 릿지($k=2$) 형태이다.

$$\sum _i{|{\beta }_i|}^k$$

더불어 둘 특징을 합친 엘라스틱넷(elastic net)도 존재하며, 하이퍼파라미터 $r$을 통해 각 기법의 영향도를 조절한다. 즉, $r$ 값이 클수록 라소(Lass, L1) 정규화 영향도가 강하고, $r$ 값이 작을수록 릿지(Ridge, L2)의 영향도가 강하다.

$$\begin{array}{rl}ElaticNe{t}^{\prime }sLC& =r\sum _{j=1}^n|{\beta }_j|+\frac{1-r}{2}\sum _{j=1}^n{\beta }_j^2\le c\end{array}$$

2.5 주성분 분석

주성분 분석(Principal Component Analysis, PCA)의 이론 근간은 선형대수학이며, 이론부터 설명하자면 고윳값과 고유벡터부턱 시작해야 한다.

주성분 분석은 정규화 기법처럼 계수 값을 줄이거나 0으로 만드는 것이 아니라, 입력변수를 다른 값으로 변환한다. 즉, 위 방법들처럼 입력 변수를 제거하여 차원을 줄이기 보다 기존 입력 변수를 표현하는 좌표축을 다른 좌표축으로 변환시킨 뒤 데이터를 가장 잘 설명할 수 있는 특정 차원들만 남긴다.

데이터를 가장 잘 설명한다는 의미는?

• 해당 변수의 분산이 크다 (참고: 입력 변수의 분산에 관한 내용)
• 왜냐하면, 변수들이 모두 하나의 값을 갖는 다면 해당 변수가 가지는 의미가 없다. 따라서 특정 입력 변수 데이터들의 분산이 커야 데이터가 가지는 의미가 있다.

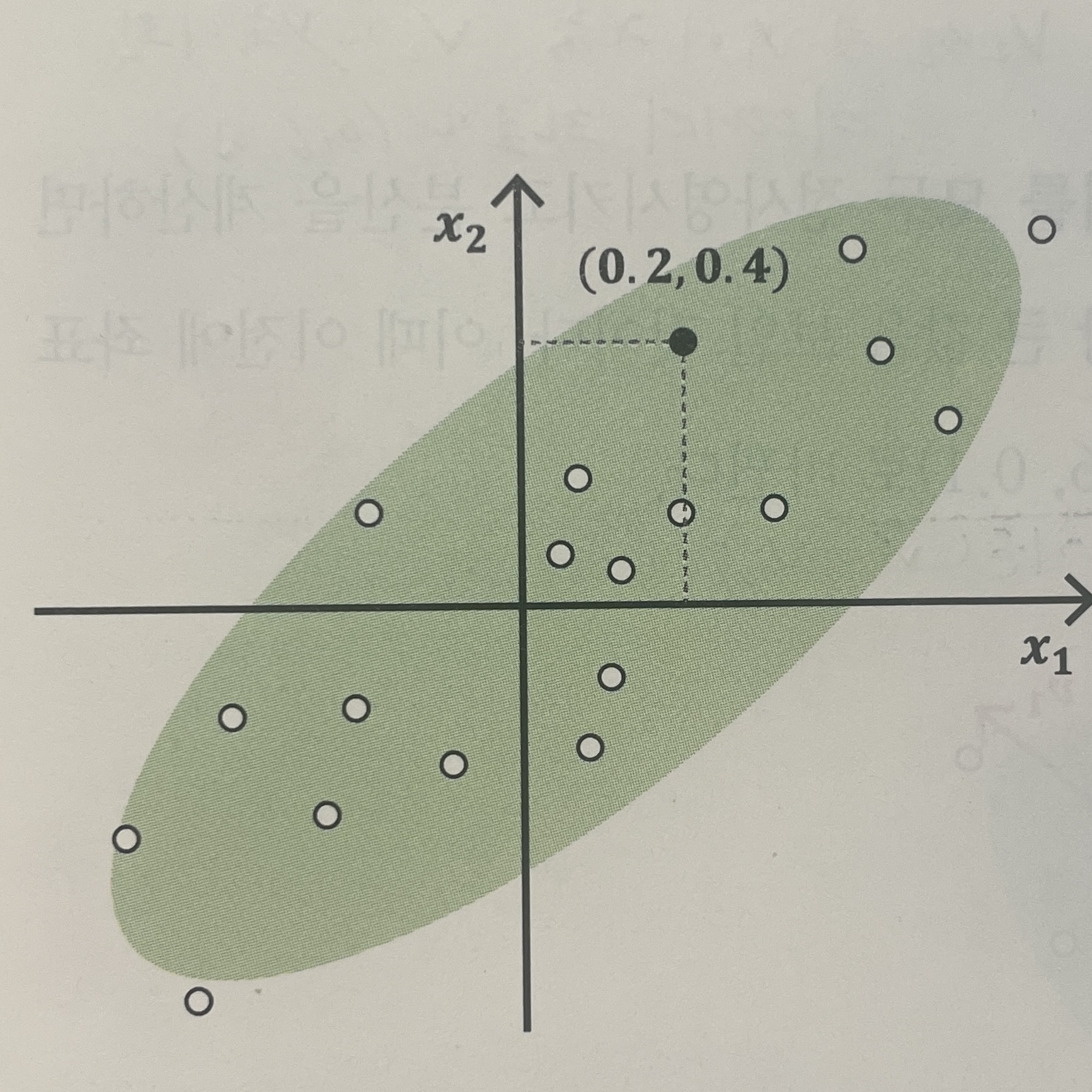
아래의 그림들을 예로 들어보자. 첫번째 그림은 기존 입력 변수 $x_1,x_2$ 2차원으로 구성되어 있으며, 이때 특정 포인트의 값이 (0.2, 0.4)이다.

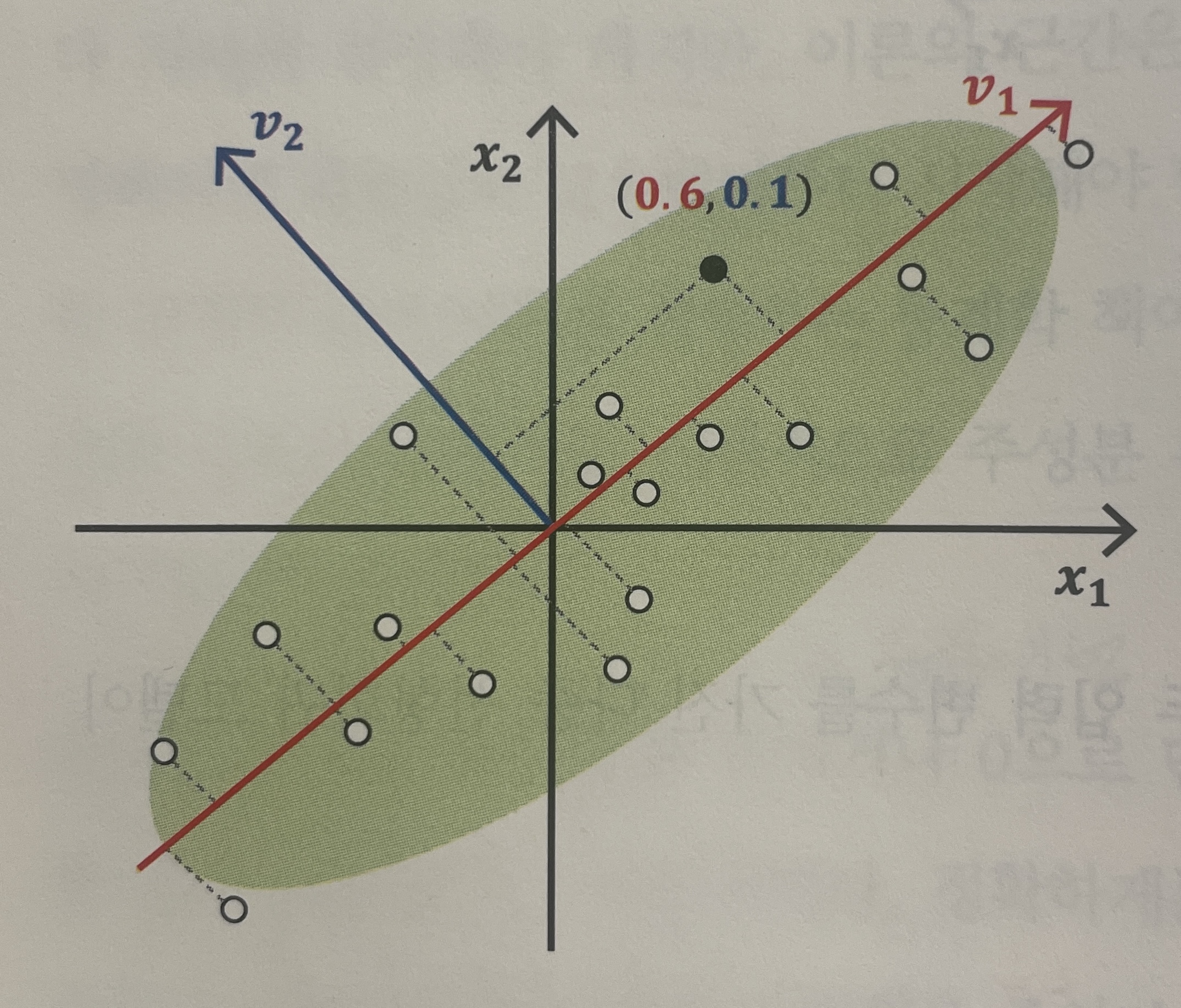
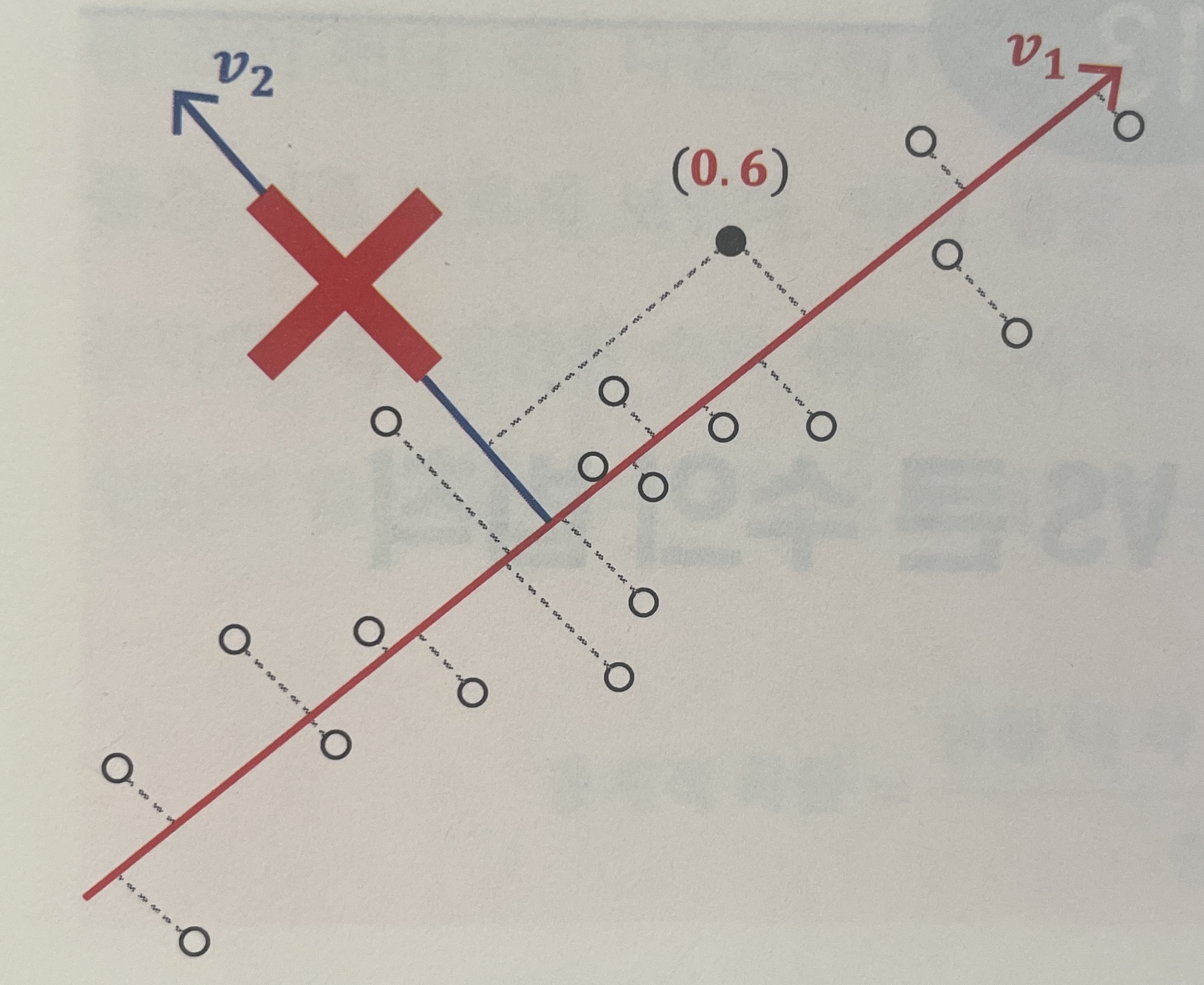
그러나 $x_1,x_2$ 축을 기준으로는 주어진 데이터를 잘 설명하지 못한다. 즉, 데이터의 분산이 크지 않다. 따라서 분산이 가장 큰 축을 찾는다면 두번째 그림과 같아진다. 새로운 축 $v_1,v_2$이 생성되고, 기존 포인트였던 (0.2, 0.4)가 새로운 축 $v_1,v_2$을 기준으로 (0.6, 0.1) 로 변환되었다.

최종적으로는 변환된 좌표축에서 큰 영향을 미치지 않는 좌표축을 제거하여 차원을 축소한다. 세번째 그림에서는 $v_2$를 제거하였다. 왜냐하면, $v_2$ 축에 데이터를 투영했을 때 분산이 $v_1$ 축에 투영했을 때 보다 분산이 작기 때문이다.

이를 입력 변수가 $p$개로 일반화 하면 다음과 같은 수식과정을 걸쳐 주성분 분석(PCA)이 된다.

• 원본: 입력 변수 $p$개
• 축 변환: PCA 통해 기존 입력 변수($x_i$) 축을 새로운 축($v_i$)으로 변환
• 차원 축소: 데이터를 잘 설명하는 축들만 남김($v_1,...,v_m$)

$$\begin{array}{rl}(원본)& y={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+...+{\beta }_p{x}_p+ϵ\\ (축변환)& y={\beta }_0^{{}^{\prime }}+{\beta }_1^{\prime }{v}_1+{\beta }_2^{\prime }{v}_2+...+{\beta }_p^{\prime }{v}_p+ϵ\\ (차원축소)& y={\beta }_0^{{}^{\prime }}+{\beta }_1^{\prime }{v}_1+...+{\beta }_m^{\prime }{v}_m+ϵ\end{array}$$

---

참고자료

• 59가지 통계학 궁금증 완전 정복