요약
- 인과성을 평가하는 대표적인 방법은 무작위 대조 실험(RCT)으로 무작위로 실험군과 대조군을 구별하여 교란자가 없도록 제어한다. 그러나 RCT는 시간과 비용이 매우 들어 현실에서 반영하기 어렵다.
- 이를 보완하기 위해 통계 모델 내 교란자를 제어하는 공변량를 새로운 입력 변수로 사용한다.
- 그 이유는 데이터의 전반적인 패턴과 그룹별로 데이터의 패턴이 일치하지 않거나 반대되는 심슨의 역설(Simpson’s paradox)로 데이터의 전반적이 패턴으로 인과성을 설명할 수 없기 때문이다.
- 그러나 공변량을 추가하여 교란자를 제어해도 그룹별로 출력변수에 영향을 미치는 정도가 다를 수 있기 때문에 상호 작용 효과도 추가적으로 고려해야 한다.
1. 개요
인과성을 평가하기 위한 방법
기존 통계분석(대표적으로 단순 선형 회귀분석)의 결과는 입력 변수와 출력 변수 간 상관관계만 확인할 수 있고, 인과관계를 논할 수 없다. 따라서, 이를 해결하기 위해 인과성을 평가하는 2가지 방법이 제시되었으며 첫 번째는 실험적 접근 방법인 무작위 대조 시험, 두 번째는 통계 모델 내 다양한 조치(공변량, 상호작용항 등) 가 있다.
2. 인과성 평가 방법
2.1 무작위 대조 시험
무작위 대조 시험(Randomized Controlled Trial, RCT)이란?
무작위로 실험군과 대조군을 구별하여 교란자같은 것들이 없도록 제어하는 시험이다. 참고사항: 연구 논문을 읽을 때 무작위 대조 시험 결과인지, 일반적인 관측 데이터에 대한 연관성 연구인지 확실히 구분해야한다. 즉, 무작위 대조 시험으로 내린 결론이어야 인과관계를 설명할 수 있다.
예를 들어, 육아를 하는 사람이 그렇지 않은 사람보다 자식과의 친밀도가 더 높은지 알고 싶다고 하자(육아 여부가 자식과의 친밀도 간 인과관계 파악).
이 때, 육아를 하는 사람은 실험군, 그렇지 않은 사람은 대조군으로 분류한 뒤 분석하면 정확한 인과관계를 설명할 수 없다. 이러한 이유는 육아를 하는 실험군 내 여성 비율이 압도적으로 높을 수 있다. 이로 인해 자식과의 친밀도가 성별의 차이인지 육아 여부의 차이인지 명확히 구분할 수 없다. 즉, 성별이라는 교란자로 인과 관계를 설명할 수 없다.
이를 해결하기 위해 교란자인 성별을 기준으로 무작위로 섞은 후, 육아를 하는 사람들을 실험군, 그렇지 않은 사람들을 대조군으로 분류한다. 단, 이후에 두 그룹 간에 또 다른 공통된 특징을 보인다면 해당 특징을 바탕으로 다시 한 번 더 무작위 과정을 거쳐야 한다. 즉, 성별(교란자1)을 기준으로 무작위로 섞은 후, 두 그룹을 나누고 그룹 간 공통된 특징(교란자2)를 기준으로 또 다시 무작위로 섞는다. 이후에 육아 여부에 따른 실험군과 대조군을 분류한다.
이렇게 실험이 세팅되었을 때 인과관계를 추론할 수 있는 통계적 세팅이 된다. 그러나 이러한 실험은 막대한 시간과 비용이 드는 문제점이 있다.
2.2 관측 데이터 활용
관측 데이터(Observational Data)란?
무작위 대조 시험과 같은 실험에서 나온 결과가 아니라 일반적으로 단순히 관측된 데이터를 의미한다.
무작위 대조 시험(RCT)는 비용이 많이 들기 때문에 효율적으로 인과관계를 평가하기 위해 관측 데이터를 활용한 통계 분석 모델에서 다양한 조치를 통해 최대한의 인과성을 추론한다. 대표적으로 회귀 분석에서 공변량을 추가한다.
이 부분을 들어가기 전에 심슨의 역설(Simpson's paradox)를 알아보자.
2.2.1 심슨의 역설
심슨의 역설(Simpson's paradox)이란?
데이터를 그룹별로 구분했을 때의 패턴과 그렇지 않은 전체 데이터의 패턴이 일치하지 않거나 반대되는 현상을 의미한다. 즉, 데이터의 전체적인 패턴과 특정 그룹별 패턴이 상이하다.
남학생과 여학생의 수학 등급과 영어 등급 간 패턴을 아래와 같다고 예를 들어보자.
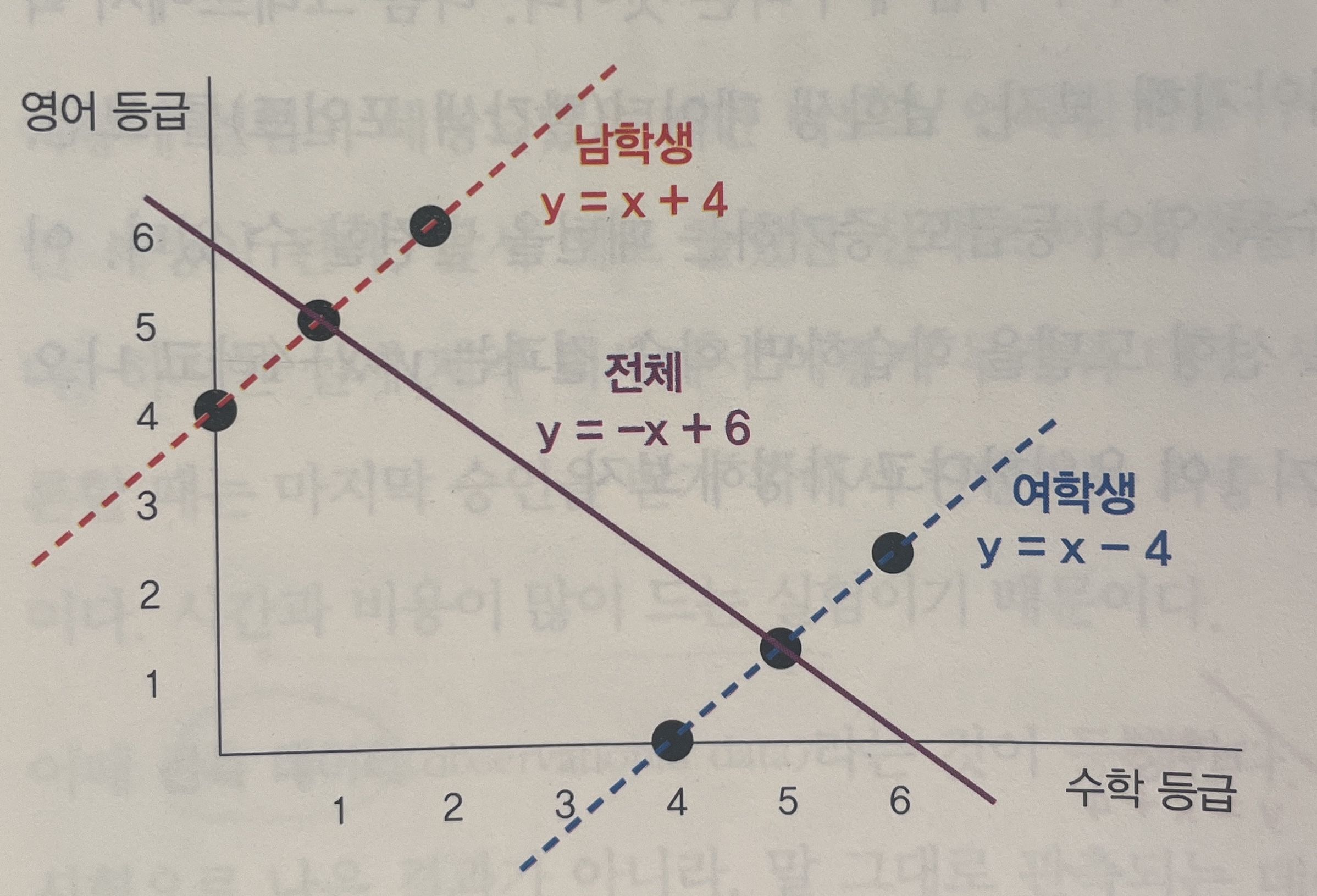
남학생과 여학생 모두 절대적인 등급(절편)만 다를 뿐 수학 등급이 증가할수록 영어 등급이 증가하는 패턴이 기울기가 1인 것으로 동일하다. 그러나 성별 구분 없이 전체적인 데이터를 기준으로 두 등급 간 관계를 살펴 보면, 수학 등급이 증가할수록 영어 등급이 감소하는 패턴인 기울기가 음수인 것으로 나타난다. 이러한 예시처럼 그룹을 구분하기 전과 후에 두 변수 간 관계가 일치하지 않거나 역전되는 현상을 심슨의 역설(Simpson’s paradox) 이라고 한다.
따라서 심슨의 역설 때문에 전체 데이터를 통해서 내린 결론이 인과가 아닐 가능성이 생긴다.
그래서 해결방안은?
앞선 내용을 다시 설명한다. 결국 성별이라는 교란자가 문제인데, 이를 제거하기 위해서는 성별을 기준으로 무작위로 섞고 실험군과 대조군을 분류한 무작위 대조 시험(RCT)이 필요하다. 그러나 이는 비용이 많이 들기 때문에 관측 데이터를 이용해서 최대한의 인과성을 추론한다. 이를 위해 공변량이라는 것을 추가하고 이는 심슨의 역설을 푸는 문제이다.
즉, 공변량은 무작위 대조 시험을 통해 교란자를 제거하는 역할과 정확히 동일하지 않지만 비슷한 효과가 있다.
2.2.2 공변량
공변량(covariate)이란?
통계 모델 학습 시 새롭게 추가되는 입력 변수이다.
앞선 수학 등급과 영어 듭급 두 변수 간의 선형 회귀식에 공변량인 성별을 추가하면 다음과 같다. 여기에 남학생은 0, 여학생은 1이라고 가정한다.
남학생의 수학 등급 값을 입력하면 를 구할 수 있다. 이렇게 산출된 계수를 기반으로 다시 여학생의 수학 등급 값을 입력하면 나머지 도 구할 수 있다.
여기서 알아야할 점은 다음과 같다. 선형 모델을 학습할 때 입력변수를 개 입력하면, 각각의 입력 변수에 대응되는 계수들은 다른 입력 변수를 고정한 상태에서 해당 입력 변수의 효과를 학습한다.
즉, 위 예시에서는 성별이 고정된 상태에서 수학 등급이 영어 등급에 얼만큼 영향을 주는지 정도를 로 학습한 것이다. 따라서 남학생, 여학생 관계없이(성별이 고정된 상태) 수학 등급은 영어 등급과 양의 관계를 가진다. 마찬가지로 수학 등급 고정된 상태에서 성별이 영어 등급에 얼만큼 영향을 주는지 정도를 로 학습했으며, 여학생(1)일수록(성별이 증가할수록) 영어 등급이 감소한다.
이처럼 해당 예시는 성별이라는 공변량을 추가하여 두 개의 선형 모델을 학습하여 차이를 반영한 것으로 볼 수 있다.
3. 한계점
위 예시에서는 남학생, 여학생 모두 수학 등급이 증가할 수록 영어 등급이 증가하는 기울기가 1로 동일하다. 그러나 두 그룹별로 수학 등급이 영어 등급에 영향을 미치는 정도가 다른 경우라면(남학생 기울기 1, 여학생 기울기 1.2)? 이러한 문제를 해결하기 위해 상호 작용 효과를 고려한다.
또한, 이러한 조치는 단순한 방법인 회귀 분석 틀 내에서 인과성을 분석하는 노력이지 무조건적인 인과라고 볼 수 없다. 잠재된 교란자들이 존재할 수 있고 입력 변수와 출력 변수가 서로 반대로 영향을 미칠 수 있는 등 복잡할 수 있다.
참고자료