요약
- 인과추론 모델이 아닌 통계 모델의 결과는 두 변수의 연관성(상관관계)을 검증하는 것이지 인과성을 검증하지 않는다.
- 연관성만 검증되는 가장 쉬운 2가지 이유는 교란자와 매개변수가 있다. 교란자는 두 변수에 모두 영향을 미쳐 변수 간 인과관계에 혼란을 주고, 매개변수는 두 변수의 인과관계 중간에 간접적으로 영향을 미치게 한다.
- 따라서, 통계 모델에서 연관성(상관관계)이 아닌 인과성을 추론하기 위해서는 구체적인 실험이나 통계 모델 내 교란자와 매개변수를 제어하는 조치를 취해야 한다.
1. 상관관계와 인과관계
Question
- 인과관계(casuation) : 두 변수가 있는 상황에서 하나의 변수는 원인이고 또 다른 변수는 결과가 되는 관계이다. 즉, 원인인 변수의 값이 변할 때 결과 변수도 변화한다.
- 상관관계(correlation) : 동일한 상황에서 변수 값의 변화 없이 두 변수의 패턴을 통해 하나의 변수가 증가할 때 또 다른 변화하는 관계이다.
예를 들어, 수학 성적이 좋은 학생이 영어 성적이 좋고, 수학 성적이 낮은 학생이 영어 성적도 낮다면 이 두 변수는 서로 상관관계가 있다고 할 수 있다.
일반적으로 통계학에서는 이러한 상관관계를 이야기한다. 그러나 원인과 결과라는 인과관계를 이야하기 위해서는 상관관계와 인과관계를 구분해야 한다.
2. 교란자와 매개변수
단순 선형 회귀분석 결과 유의
이 분석의 결과가 통계적으로 유의미하다는 의미는 두 변수가 상관관계에 있다는 증거이지, 인과관계에 대한 증거는 아니다.
예를 들어, 수학 성적이 영어 성적에 영향을 주는 지 단순 선형 회귀 분석 결과가 통계적으로 유의미하다고 하자. 이때 두 변수 간 실제로 인과관계로 인해 상관관계가 있을 수 있다. 그러나 인과관계가 있는지는 알 수 없다.
Question
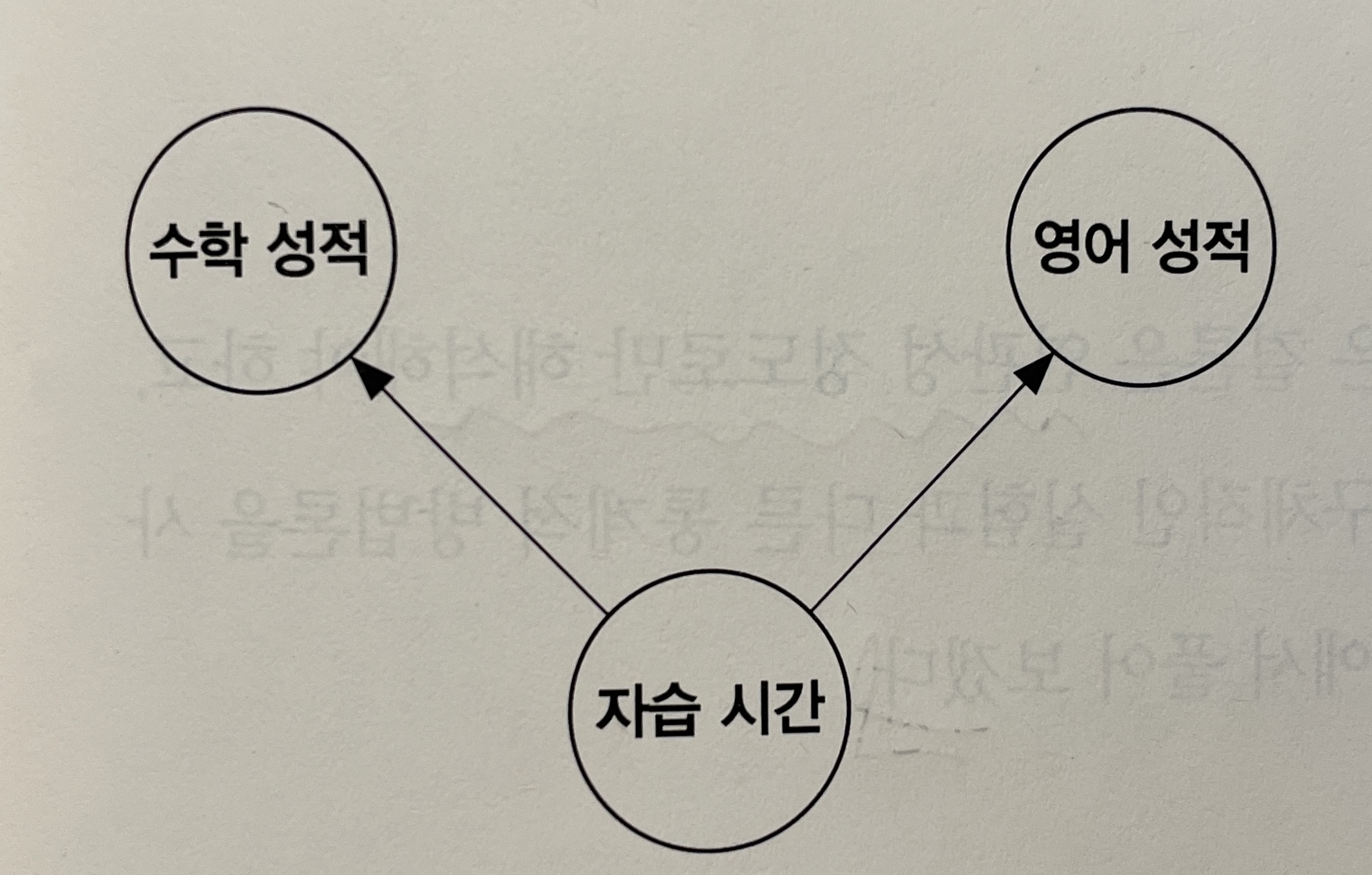
- 교란자(confounder): 입력 및 출력변수 모두에게 영향을 주는 제3의 변수로 두 변수 사이의 인과관계를 혼란을 준다.
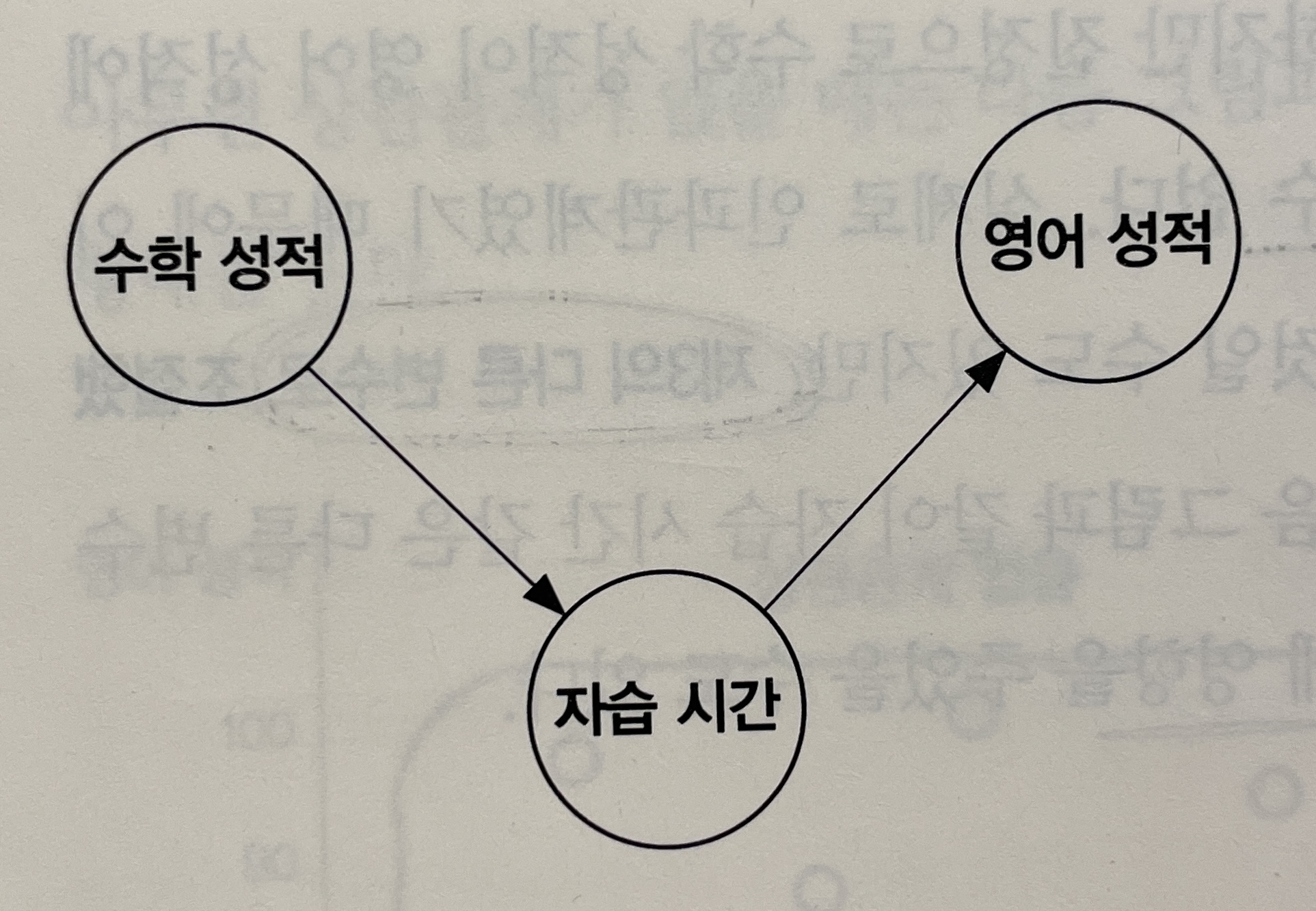
- 매개변수(Intermediate variable): 입력 및 출력 변수 간 직접적인 관계가 아닌 또 다른 변수로 인해 간접적인 영향을 미치는 변수이다.
예를 들어, 두 변수가 아닌 자습시간이라는 또 다른 변수가 두 변수 모두에게 영향을 미칠 수 있다. 이로 인해 수학 성적과 영어 성적 사이에 인관성은 없지만, 자습시간이라는 교란자로 분석 결과만 봤을 때 관계가 있어 보일 수 있다. 따라서 두 변수 사이에 상관관계는 확인할 수 있지만, 인과관계는 확인할 수 없다.
또한, 수학 성적이 자습 시간에 영향을 주고 자습 시간이 영어 성적에 영향을 줄 수도 있다. 이때 입력 변수인 수학 성적은 출력 변수인 영어 성적에 간접적으로 영향을 주었다고 볼 수 있다. 이를 간접 효과라고 한다.
따라서, 통계분석에서 얻은 결론은 연관성(= 상관관계) 정도로만 해석하고 인과성은 구체적인 실험과 다른 통계적 방법론을 사용해야 한다.
참고자료