(Algorithm) 커널 밀도 추정(KDE, Kernel Density Estimation)

요약

• 커널 밀도 추정은 데이터가 특정 분포를 따른다는 가정 없이 관측된 데이터만으로 확률 밀도 함수를 추정하여 전체적인 분포 형상을 파악하는 방법임.
• 커널은 적분값이 일이고 대칭인 비음수 함수를 뜻하며 가우시안과 같은 함수를 각 데이터 지점마다 씌워서 개별적인 분포를 만듦.
• 최종적인 밀도 추정은 모든 관측치에 적용된 커널 함수들을 합산하고 평균을 내어 히스토그램보다 부드러운 곡선 형태를 도출하는 과정임.
• 대역폭 파라미터는 커널의 폭을 조절하는데 값이 너무 작으면 과적합되어 곡선이 뾰족해지고 너무 크면 데이터의 특징이 뭉개질 수 있어 적절한 설정이 중요함.
• 이때 도출된 값은 특정 구간의 확률을 의미하는 면적이 아니라 해당 값이 분포 내에서 얼마나 밀집되어 나타나는지를 보여주는 밀도 추정치임.

---

1. 개요

배경 및 목적

1. 배경
2. 데이터의 분포를 파악하는 것은 데이터 분석에서 매우 중요한 단계이다.
3. 실제 데이터는 정규분포를 따르지 않고 어떤 분포를 따르는지 알 수 없다.
4. 목적
5. 따라서, 데이터의 분포를 추정하여 확률 밀도(Proability Density)를 구한다.
6. 이를 위한 방법으로 Histogram, Kernel Density Estimation, K-nearest neighbor 등 방법이 존재한다.

---

2. KDE 이란?

2.1. 커널(Kernel)이란?

분야마다 Kernel을 달리 정의하지만, 본문에서는 KDE에서의 Kernel의 의미를 파악함

2.1.1 정의

수학적으로 Kernel 의 정의는 다음과 같다.

1. 적분값이 1
2. 비음수(non-negative) 함수
3. 모든 값이 대칭

$$\begin{array}{rl}& \int K(u)du=1;\\ & K(-u)=K(u)\text{for all values of}u\end{array}$$

따라서, 위 수식을 만족하는 함수를 모두 Kernel 함수라고 정의할 수 있다.

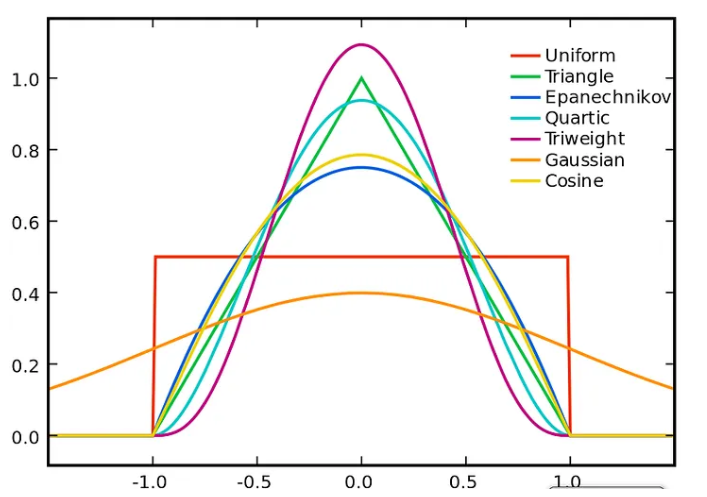
대표적인 커널 함수의 종류로는 Gaussian, Uniform, Epanechnikov 등이 있으며, 분석에 활용하는 데이터의 특성을 고려하여 선택할 수 있다. 즉, 커널 함수 안에서 정의된 확률변수(RV) $x$를 $K(x)$ 라고 한다.

2.1.2 분류

커널함수 선택

데이터의 특성을 고려하여 분석 목적에 맞는 커널함수를 선택 예를 들어, 공간 상의 포인트들에 매출액 정보가 존재할 때 해당 포인트들의 매출 정보를 활용하여 상권의 범위를 파악하고자 한다. 이 때 높은 매출액이 집중된 형태를 파악하고 싶다면, 중심성이 강한 커널함수를 적용하는 것이 효율적이다. 따라서, 일반적으로 활용되는 Gaussian도 좋지만, Epanechnikov나 Triangle 등을 활용할 수 있다. 더 나아가 계산의 효율성이나 해석의 용이성 등을 고려하여 최종적으로 커널 함수를 선택할 필요가 있다.

커널함수	형태	특징
Quartic	$(1-u^2{)}^2$	부드러운 종 모양, 밀도 추정에 자주 활용
Triangular	$1-\Vert u\Vert$	중심에서 멀어질수록 선형감소, 단순하고 계산 효율 좋음
Triweight	$(1-u^2{)}^3$	Quartic 보다 가장자리가 완만해 이상치에 강함
Epanechnikov	$(1-u^2)$	이론적으로 MSE 최소형태, 계산 효율이 높고 가장 널리 사용됨

2.2밀도 추정(Density Estimation)란?

밀도 추정은 데이터를 통해 확률변수(RV)의 특성을 추정하는 것을 목적으로 둔다. 즉, 관측된 데이터로부터 변수가 가질 수 있는 모든 값의 확률(밀도)를 추정한다.

관측치 $x$의 밀도를 추정하는 것은 $x$의 PDF를 추정하는 것과 같다.

아래 확률밀도함수(PDF) $f(x)$가 존재할 때, $f(a)$는 $x=a$ 에서 확률밀도(Probability Density) 이며, $f(a)$ 값의 의미는 확률변수($x$)가 $a$ 가 될 가능성을 의미한다.

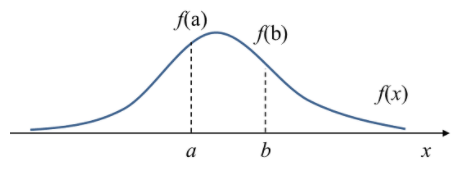
밀도는 확률과 유사한면이 있지만 엄연히 다른 개념으로 비교해서 이해해야 한다.

여기서 $x=a$ 에서의 확률은 다음과 같다.

$${\int }_{x=a}^{a}f(x)dx$$

위 적분값이 0 이므로 확률값 또한 0이 된다. 그러나 $x=a$에 대한 Density는 $f(a)$로 0이 아니다! 즉, 확률은 $x$ 가 $a-b$구간의 적분값인 면적을 의미하지만, Density는 PDF의 함수값이고 이 구간에 대해 적분하면 PDF가 나오게 됨

2.3. 그래서 KDE(Kernel Density Estimation) 란?

커널 함수(Kernell Function)를 이용하여 밀도를 추정(Density Estimation) 하는 것을 의미한다. 즉, 커널 함수의 세계에서 확률변수(RV)를 추정하는 것을 의미한다.

KDE의 수식은 아래와 같다.

$$\widehat{f_h}(x)=\frac{1}{nh}\sum _{i=1}^{n}K(\frac{(x-x_i)}{h})$$

2.3.1. $h$ 의미

여기서 $h$는 커널을 조정하는 주요 파라미터로 대역폭(bandwidth) 라고 하며, 히스토그램의 bin 크기로 이해하면 된다. 대역폭($h$)을 통해 커널의 첨도를 결정함

대역폭이 너무 낮은 경우, 곡선이 들쑥날쑥하는 등 데이터에 너무 민감하여 과적합 발생 높은 경우, 개별 데이터 간 차이가 사라짐

첨도(kurtosis)란?

• 분포의 뾰족한 정도를 의미한다. 즉, 평균 주변으로 얼마나 뾰족하게 집중되었는지를 의미함
• 첨도가 클수록 평균 주변으로 뾰족하고 날카롭게 형성

2.3.2. 시그마 의미

시그마 = $\frac{1}{n}{\sum }_{i=1}^{n}K(x-x_i)$

위 수식의 의미는 커널함수가 적용된 관측치들의 평균이다. 즉 분포의 평균을 의미한다.

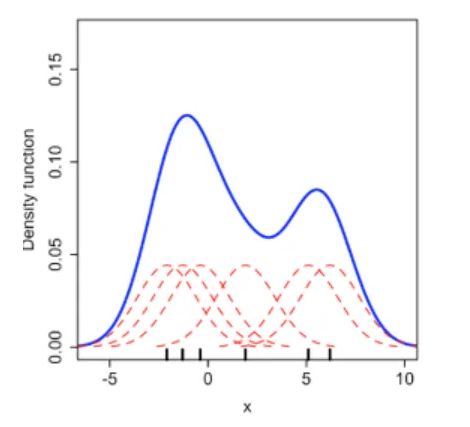
이를 시각화 하면 다음과 같다. 빨간색 점선의 분포는 각 확률변수 $x_i$ 에 대한 커널 함수들의 분포이다. 이는 $x_i$가 가질 수 있는 모든 값에 대한 확률(밀도)이다. 파란색 실선의 분포는 다양한 빨간색 점선 분포들의 평균이다.

즉, 각 빨간색 점선의 커널함수를 모두 더한 후 전체 데이터 개수로 나눈 값이다.

따라서, KDE는 기존 히스토그램에 비해 훨씬 부드러운 곡선을 나타내며, 파라미터인 대역폭($h$)에 따라 첨도가 조금씩 달라지므로 최적의 값을 선정해야 한다.

---

3. 결론

내가 이해한 바를 조금 더 자세히 적어보겠다. <현재> 데이터의 분포를 모를 때, 비모수적 확률밀도함수를 추정하기 위해 활용한다.

각 변수에 일반적으로 가우시안 커널을 인위적으로 얹는다. 이 때 생성된 n개의 가우시간 커널을 합치고 정규화하여 최종적으로 커널밀도추정 함수(KDE)를 생성한다.

생성된 KDE에 기존 변수값을 넣었을 때 나오는 값이 그 지점에 대한 확률밀도 추정치이다. 이때 이는 확률이 아니다! 확률은 특정 구간에서의 적분값이다. 단순한 함수값은 확률밀도 추정치이다.

따라서, 이때의 함수값은 데이터 분포를 고려했을 때 그 값이 얼마나 자주 나타날 확률밀도인가를 의미함

<과거> $K(u)$는 결국 평균을 중심으로 대칭된 분포를 나타낸다. $u$의 절댓값이 커질수록 커널함수 값은 0에 가까워 진다.

즉, 맨 오른쪽 관측치의 커널함수를 보면 왼쪽 관측치들에 대한 커널함수값은 거의 0이다. 그래서 $x_i$는 먼 관측치들의 영향을 거의 고려하지 않는다.

그리고 $u$ 값을 조절하기 위해 $h$를 활용한다. $h$ 값을 증가시키면, 기준점으로부터 먼 관측치들의 영향을 더 고려하겠다는 의미가 된다.

반대로 $h$값을 감소시키면, 기준점으로부터 가까운 관측치들의 영향을 더 중요하게 고려하겠다는 의미가 된다.

---

참고사이트

• 커널 밀도 추정
• KDE 이란?
• 커널밀도함수
• 스타벅스로 풀어보는 공간데이터 사이언스 - 커널함수