요약
- 교란자를 제어하는 공변량별로 출력 변수에 미치는 영향 정도가 다를 수 있기 때문에 기존 입력 변수와 공변량을 동시에 고려하는 상호 작용 효과라는 새로운 변수를 모델에 추가한다.
- 즉, 상호 작용 효과로 인해 그룹별로 출력 변수에 영향을 미치는 정도(기울기 또는 계수)를 따로 학습할 수 있다.
- 물론 이를 고려하여도 명확한 인과성이 아닌 연관성으로 해석해야 하지만, 나름 상대적인 인과성을 추론할 수 있다.
- 그러나 이처럼 인과성 추론을 위해 공변량과 상호 작용 효과를 추가해도 우리가 모르는 교란자들이 존재할 수 있고, 무작정 변수들을 추가하면 학습해야하는 계수가 증가하여 모델이 복잡해진다.
1. 개요
앞선 단계에서 교란자를 제어하기 위해 공변량인 성별을 입력 변수로 추가하였다. 그러나 성별에 따라 입력 변수와 출력 변수 간 상관성 정도(계수)가 다르다면 입력 변수와 공변량을 곱한 상호 작용 효과를 추가적으로 고려해야 한다. 아래 수식은 상호 작용 효과를 추가한 모델이다.
남학생과 여학생의 수학 등급과 영어 등급 간 패턴을 아래와 같다고 예를 들어보자.
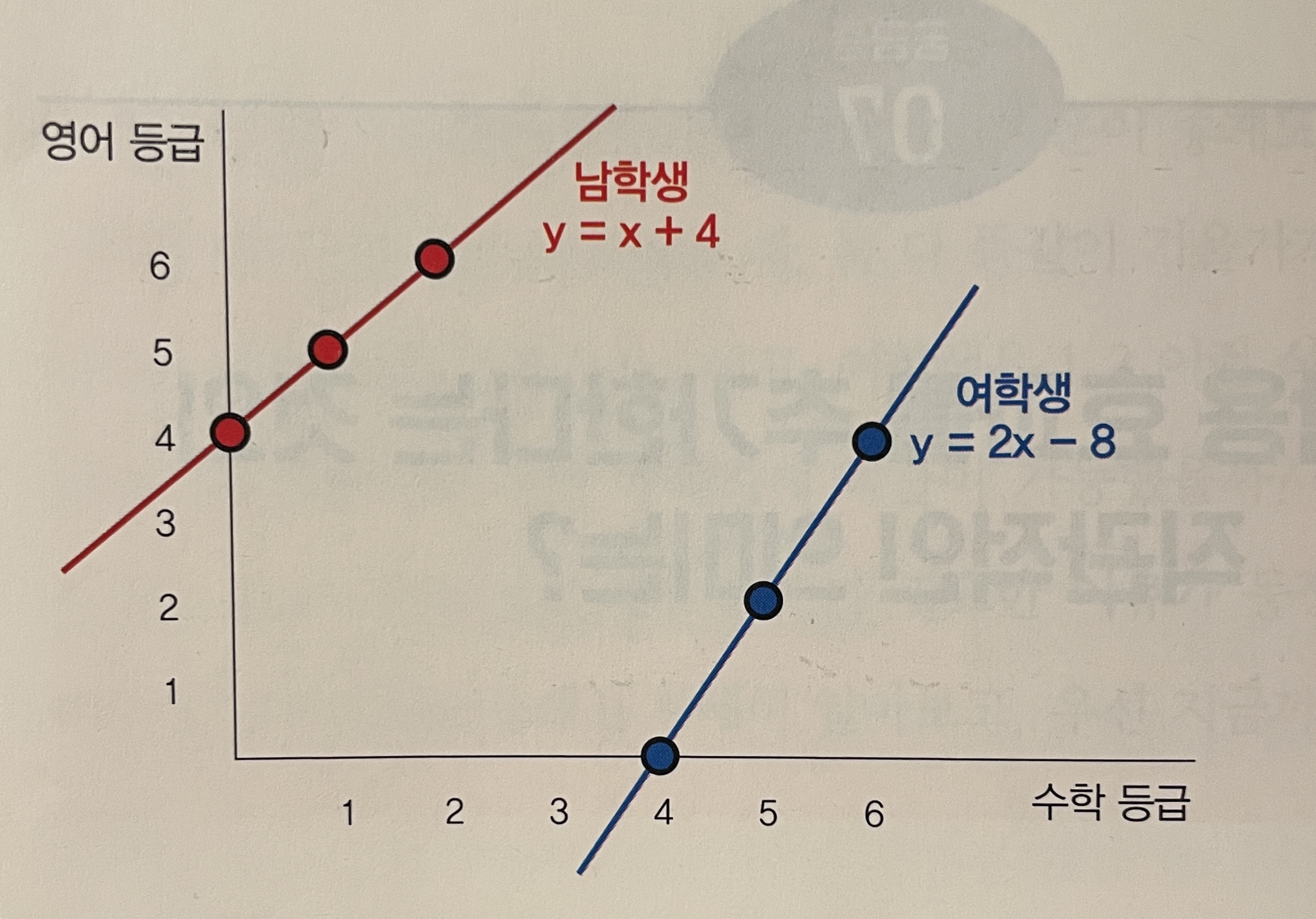
2. 상호 작용 효과
상호 작용 효과란?
입력 변수와 공변량을 곱한 새로운 입력 변수이다. 결국 무작위 대조 시험이 아닌 관측 데이터를 통한 통계 모델 내 조치를 통해 인과관계를 최대한 추론하기 위함이다.
2.1 활용
남학생 값 (성별 = 0) 입력을 통해 위 수식에서 을 학습할 수 있다. 이렇게 학습된 계수를 수식에 입력한 후 여학생 값(성별 = 1)을 입력하면 다음과 같이 수식이 성립된다. 은 여학생 자료만 고려했을 때 수학 등급 과 영어 등급 간 연관성 정도의 기울기를 의미한다.
즉, 상호 작용 효과를 통해 다른 그룹의 기울기를 따로 학습할 수 있다. 다시 정리 하면 단순히 성별이라는 공변량만을 고려하면 실제로 성별에 따라 입력 변수와 출력 변수의 기울기가 다르다는 점을 찾지 못한다. 따라서 공변량과 입력 변수를 곱한 상호 작용 효과를 새로운 입력 변수로 추가한 모델을 학습한다. 이를 통해 성별에 따라 입력 변수와 출력 변수 간 연관성 정도인 기울기를 각각 학습할 수 있다.
위 모델의 계수들이 의미하는 바를 정리하면 다음과 같다.
- : 남학생의 수학 등급이 영어 등급에 영향을 미치는 연관성 정도
- 왜? 남학생의 성별 값이 0 이므로 수학 등급에 대한 계수만 산출된다.
- : 성별이 영어 등급에 영향을 미치는 연관성 정도
- 왜? 성별이라는 공변량에 대한 계수로 다른 변수가 고정된 상태에서 성별이 출력 변수와의 연관성을 의미한다.
- : 여학생의 수학 등급이 영어 등급에 영향을 미치는 연관성 정도
- 왜? 여학생의 성별 값이 1 이므로 성별과 수학 등급이 모두 고려되었다.
- : 남학생의 수학 등급이 0 일 때의 영어 등급으로 즉, 남학생 자료의 절편이다.
2.2 결론 및 한계점
이처럼 자료를 특정한 그룹으로 나누고 그룹 내에 연관성 정도가 서로 다른 것을 고려하여 모델을 학습하고자 한다면 단순히 공변량을 추가하는 것이 아니라 공변량과 본래 입력 변수 사이의 상호 작용 효과를 추가적으로 고려해야 한다. 추가로 다른 공변량인 입력 변수들을 추가하거나 가능한 모든 조합인 상호 작용 효과를 추가할 수 있다. 그러나 변수의 수가 많아지면 학습해야할 계수가 증가하고 모델이 복잡해진다.
따라서, 적합한 계수를 학습하기 위해 충분한 데이터의 양과 사전 지식 등을 통해 정말 필요한 경우에만 상호 작용 효과를 추가하는 것을 권장한다.
또한, 위 활용에서 모델의 결과를 연관성 정도로만 해석하였다. 인과성이라고 하지 않은 이유는 숨은 교란자들이 존재할 수 있기 때문이다. 그렇지만 이처럼 적절한 공변량과 상호 작용 효과를 추가하여 교란자를 제어한다면 상대적으로 인과성을 추론할 수 있다.
참고자료